Here is the beginning of an exhausting explanation …
The Greeks realized that sounds which have frequencies in rational proportion are perceived as harmonius. For example, a doubling of frequency gives an octave. A tripling of frequency gives a perfect fifth one octave higher. They didn’t know this in terms of frequencies, but in terms of lengths of vibrating strings. Pythagoras, who experimented with a monochord, noticed that subdividing a vibrating string into rational proportions produces consonant sounds. This translates into frequencies when you know that the fundamental frequency of the string is inversely proportional to its length, and that its other frequencies are just whole number multiples of the fundamental. (actually, the notion of consonance is more complicated than rationality- see, for example, this fascinating article ).
First, we should examine what ratios are “meant” to exist in the western scale. The prominence of the major triad in western music reflects the Greek discoveries mentioned above. Starting with the note C as a fundamental, we get the major triad from the 3rd and 5th overtones, dropping down one and two octaves respectively, obtaining ratios of 3/2 (G:C) and 5/4 (E:C) respectively. Two other prominent features in western music include the V I cadence, and the I,IV,V triads. Both reflect the importance of the 3/2 ratio, with the IV further taking into account the reciprocal of 3/2, namely 2/3 aka 4/3. Musically, the reciprocal ratio corresponds to going down rather than up. While 3/2 corresponds to going up a fifth, 2/3 corresponds to going down a fifth, and 4/3 corresponds to going down a fifth and up an octave. Together, 3/2 and 4/3 divide the octave, so that going up by 3/2 followed by 4/3 gives an octave.
The IV and V triads give us the four new notes, B and D of G,B,D, and F and A of F,A,C. Their ratios, relative to C are 15/8 for B, 9/8 for D, 4/3 for F, and 5/3 for A. The notes formed from the I,IV, and V major triads produce the C major scale: C D E F G A B C. Throwing in reciprocals for each of these intervals yields all the intervals that made up western music until the rise of chromaticism.
1/1 unison C
2/1 octave C
3/2 perfect fifth G
4/3 fourth F
5/4 major third E
8/5 minor 6th Ab
6/5 minor 3rd Eb
5/3 major 6th A
9/8 major 2nd D
16/9 minor 7th Bb
15/8 major 7th B
16/15 minor 2nd C#
While this list of intervals does include a few of the most basic intervals and their reciprocals: unison, perfect 5th, major 3rd, major 6th = 3rd above a 4th (or also a 4th above a 3rd), major 2nd = a 5th above a 5th, and major 7th = a 3rd above a 5th (or also a 5th above a 3rd), some obvious ones are missing (such as 7/4, 25/16 = a 3rd above a 3rd, or 9/5 = a fifth above a minor 3rd).
The tritone (such as C to F#) is also omitted from this list, an interval that did not affect the evolution of the western scale as it was not used in western music until twelve note chromaticism had become firmly established. Actually, a tritone refers to two different possible intervals:
7/5 tritone
10/7 also called a tritone.
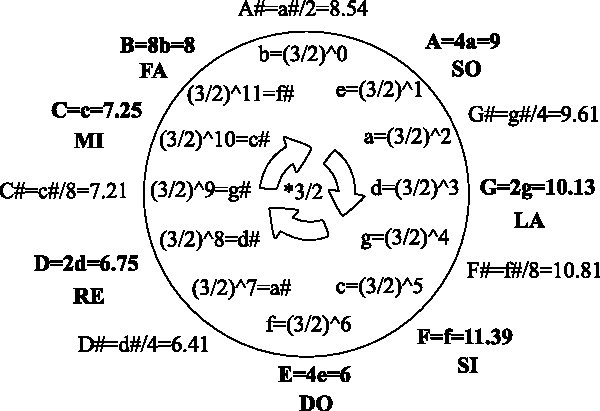
The idea behind twelve is to build up a collection of notes using just one ratio. The advantage to doing so is that it allows a uniformity that makes modulating between keys possible. Without a compromise most keys would be unusable as most of the basic intervals would not be captured in the different keys (see the table at the end of this essay).
Unfortunately, no one ratio will do the trick exactly. However, the ratio of 3/2 happens to work reasonably well using 12 steps. With 3/2 as the basis for the scale, none of the above ratios besides a unison, fifth, and major 2nd are captured exactly.
However the most important constraint- namely that we get a repeating pattern going up in octaves, is almost satisfied by this scheme. Namely, after 12 applications of the ratios 3/2, we come back very close to where we started from (always dropping down by an octave, i.e. dividing by 2, each time the ratio exceeds 2):
(3/2)^0 = 1
(3/2)^1 = 1.5
(3/2)^2 = 1.125 (after dividing by 2)
(3/2)^3 = 1.6875 (after dividing by 2)
(3/2)^4 = 1.2656 (after dividing by 4)
(3/2)^5 = 1.8984 (after dividing by 4)
(3/2)^6 = 1.4238 (after dividing by 8)
(3/2)^7 = 1.0678 (after dividing by 16)
(3/2)^8 = 1.6018 (after dividing by 16)
(3/2)^9 = 1.2013 (after dividing by 32)
(3/2)^10 = 1.8020 (after dividing by 32)
(3/2)^11 = 1.3515 (after dividing by 64)
(3/2)^12 = 1.0136 (after dividing by 128)
we have returned close to where we started from. (these 12 frequencies correspond to the circle of 5ths. Starting from C, we then get G D A E B F# C# Ab Eb Bb F and back to C).